https://colab.research.google.com/drive/1ZRtXkgNDCZ74AX5PGn8ScD3izxkhu07P?usp=sharing
PA03_202155646_문진혁.ipynb
Colab notebook
colab.research.google.com
Problem
부산대학교 컴퓨터공학과 학생인 산지니는 봉사 동아리에 들어가 주기적으로 농촌 봉사를 하고 있다.
밀밭에서 열심히 일을 하던 산지니는 여러 가지 밀 씨앗들을 보며 이러한 데이터도 머신러닝에 적용하면
재밌겠다고 생각했다. 산지니는 이번에도 “머(신러닝)잘알(아)” 친구인 당신에게 도움을 요청했다. 머알못
산지니를 위해 이전 수업에서 배운 모델과 지식을 활용하여 도움을 주자.
입력
• 씨앗의 정보가 담긴 CSV 파일 “seeds.csv”가 주어진다. • 출력
• CSV 파일 안에 있는 씨앗의 정보를 적절히 활용하여 주어진 예측을 수행하자. • 제한
• Todo 1, 2를 모두 구현해야 한다.
Dataset
• Dataset Preview
• “seeds.csv”
• 세 가지 다른 밀 품종인 Kama, Rosa 및 Canadian에 대한 정보가 담겨 있습니다.
• 210 rows x 7 columns



TODO 1
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
# 데이터 확인
data = pd.read_csv('seeds.csv')
data
scaler = StandardScaler()
scaled_data = scaler.fit_transform(data.iloc[:, :-1])
pca = PCA(n_components=2)
pca_data = pca.fit_transform(scaled_data)
# 시각화 PCA of Seed Data
plt.figure(figsize=(10, 7))
plt.scatter(pca_data[:, 0], pca_data[:, 1])
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')
plt.title('PCA of Seed Data')
plt.show()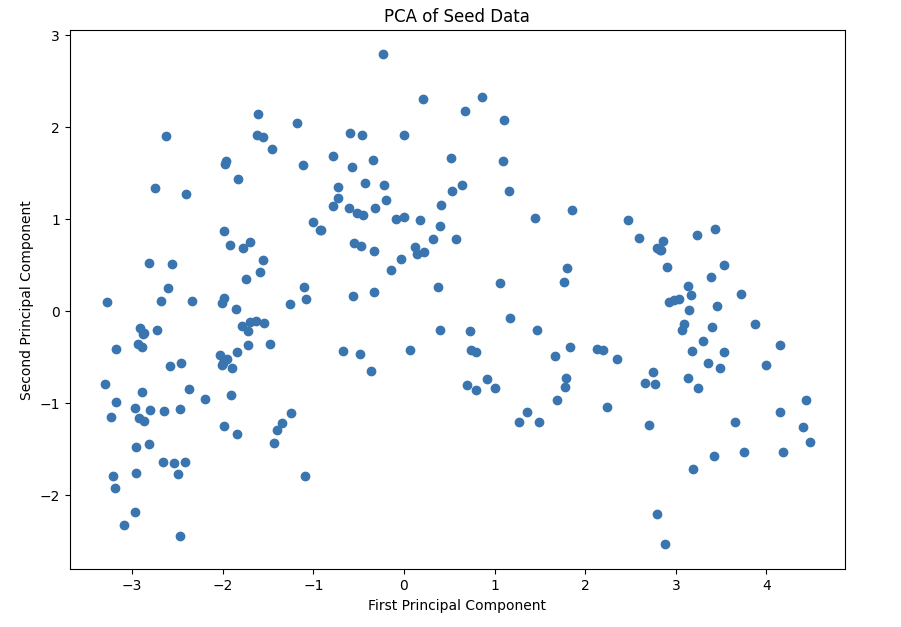
wcss = []
for i in range(1, 11):
kmeans = KMeans(n_clusters=i, init='k-means++', max_iter=300, n_init=10, random_state=0)
kmeans.fit(pca_data)
wcss.append(kmeans.inertia_)
plt.figure(figsize=(10, 7))
plt.plot(range(1, 11), wcss)
plt.title('Elbow Method')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS')
plt.show()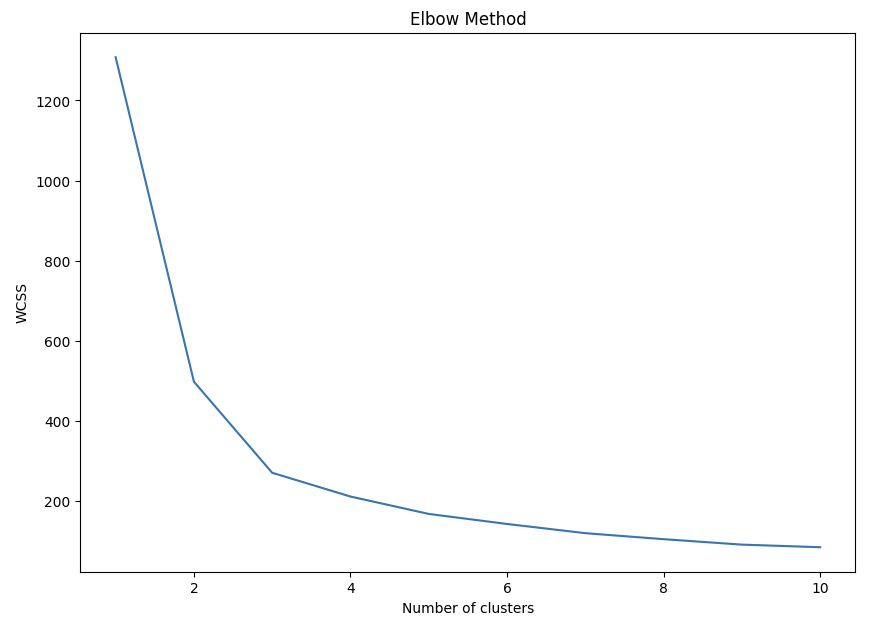
kmeans = KMeans(n_clusters=3, init='k-means++', max_iter=300, n_init=10, random_state=0)
clusters = kmeans.fit_predict(pca_data)
plt.figure(figsize=(10, 7))
plt.scatter(pca_data[:, 0], pca_data[:, 1], c=clusters, cmap='viridis')
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')
plt.title('Clusters of Seed Data')
plt.show()
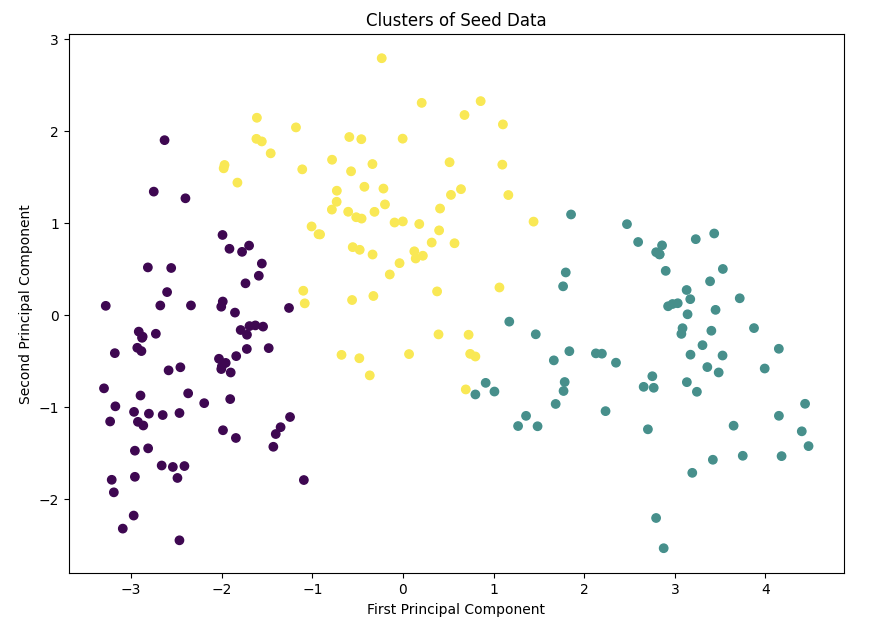
TODO 2
from sklearn.linear_model import Ridge, LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
data = pd.read_csv('seeds.csv')
X = data.iloc[:, :-1].values
y = data.iloc[:, -1].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
ridge_reg = Ridge(alpha=1.0)
ridge_reg.fit(X_train, y_train)
y_pred_ridge = ridge_reg.predict(X_test)
lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)
y_pred_lin = lin_reg.predict(X_test)
mse_ridge = mean_squared_error(y_test, y_pred_ridge)
mse_lin = mean_squared_error(y_test, y_pred_lin)
print(f'Ridge Regression MSE: {mse_ridge}')
print(f'Linear Regression MSE: {mse_lin}')
from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=1.0)
lasso_reg.fit(X_train, y_train)
y_pred_lasso = lasso_reg.predict(X_test)
mse_lasso = mean_squared_error(y_test, y_pred_lasso)
print(f'Lasso Regression MSE: {mse_lasso}')
from sklearn.linear_model import Ridge, LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import pandas as pd
# 데이터 로드 및 전처리
data = pd.read_csv('seeds.csv')
X = data.iloc[:, :-1].values
y = data.iloc[:, -1].values
# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# Ridge Regression 모델 학습 함수: alpha 값을 인자로 받음
def train_ridge_regression(alpha_value):
ridge_reg = Ridge(alpha=alpha_value)
ridge_reg.fit(X_train, y_train)
y_pred_ridge = ridge_reg.predict(X_test)
mse_ridge = mean_squared_error(y_test, y_pred_ridge)
return mse_ridge
# Linear Regression 모델 학습 및 성능 평가
lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)
y_pred_lin = lin_reg.predict(X_test)
mse_lin = mean_squared_error(y_test, y_pred_lin)
# Ridge Regression의 성능 평가: 여러 alpha 값에 대해 MSE 계산
alpha_values = [0.01, 0.1, 1.0, 10.0, 100.0]
for alpha_value in alpha_values:
mse_ridge = train_ridge_regression(alpha_value)
print(f'Ridge Regression MSE with alpha={alpha_value}: {mse_ridge}')
print(f'Linear Regression MSE: {mse_lin}')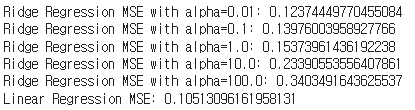
TODO 1
K-means 클러스터링을 사용하여 데이터를 클러스터링합니다.
적절한 클러스터 수를 선택하기 위해 엘보우 방법(Elbow method)을 사용합니다.
PCA를 통한 차원 축소
scikit-learn의 PCA를 사용하여 데이터의 차원을 2차원으로 축소했습니다. 이를 통해 데이터를 시각화하고 분석하기 용이하게 만들었습니다. PCA 결과, 주요 두 성분이 데이터 분산의 상당 부분을 설명하는 것으로 나타났습니다.
TODO 2
Ridge Regression은 선형 회귀에 L2 규제를 추가한 모델입니다. 규제 강도는 alpha 매개변수로 조절할 수 있습니다.
Ridge Regression 모델의 MSE는 Linear Regression 모델의 MSE보다 낮게 나타났습니다. 이는 Ridge Regression이 데이터의 복잡성을 더 잘 처리하고, 과적합을 방지하는 데 효과적임을 시사합니다.
추가로 ridge를 사용하는 방법도 있지만 lasso 방법을 사용해볼 수 있습니다
사용법이 간단하여 시도해보겠습니다
0.01일 때 가장 mse가 낮으므로 성능이 제일 좋았고 신기하게 선형회귀일 때 mse가 가장 낮게 나왔습니다.
결론
밀 씨앗 데이터셋을 활용하여 클러스터링 및 차원 축소, 그리고 Regularization을 사용한 회귀 분석을 수행했습니다. PCA와 K-means 클러스터링을 통해 데이터의 구조를 이해할 수 있었습니다. 또한, Ridge Regression을 통해 데이터의 복잡성을 효과적으로 처리하고, 모델의 성능을 향상시킬 수 있었습니다. 추가로 lasso보다는 ridge의 mse 성능평가의 결과가 더 좋았습니다. 알파값의 조정에서는 낮을 값이 좀 더 좋은 성능을 나타내기도 하였습니다.
'프로젝트 > 머신러닝 과제' 카테고리의 다른 글
| [ML Project] EDA 데이터 분석 with SVM, PM, Decision Tree (2) | 2024.04.25 |
|---|---|
| [ML Project] Linear Regression을 활용한 주가 예측 모델 (0) | 2024.04.11 |
https://colab.research.google.com/drive/1ZRtXkgNDCZ74AX5PGn8ScD3izxkhu07P?usp=sharing
PA03_202155646_문진혁.ipynb
Colab notebook
colab.research.google.com
Problem
부산대학교 컴퓨터공학과 학생인 산지니는 봉사 동아리에 들어가 주기적으로 농촌 봉사를 하고 있다.
밀밭에서 열심히 일을 하던 산지니는 여러 가지 밀 씨앗들을 보며 이러한 데이터도 머신러닝에 적용하면
재밌겠다고 생각했다. 산지니는 이번에도 “머(신러닝)잘알(아)” 친구인 당신에게 도움을 요청했다. 머알못
산지니를 위해 이전 수업에서 배운 모델과 지식을 활용하여 도움을 주자.
입력
• 씨앗의 정보가 담긴 CSV 파일 “seeds.csv”가 주어진다. • 출력
• CSV 파일 안에 있는 씨앗의 정보를 적절히 활용하여 주어진 예측을 수행하자. • 제한
• Todo 1, 2를 모두 구현해야 한다.
Dataset
• Dataset Preview
• “seeds.csv”
• 세 가지 다른 밀 품종인 Kama, Rosa 및 Canadian에 대한 정보가 담겨 있습니다.
• 210 rows x 7 columns



TODO 1
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
# 데이터 확인
data = pd.read_csv('seeds.csv')
data
scaler = StandardScaler()
scaled_data = scaler.fit_transform(data.iloc[:, :-1])
pca = PCA(n_components=2)
pca_data = pca.fit_transform(scaled_data)
# 시각화 PCA of Seed Data
plt.figure(figsize=(10, 7))
plt.scatter(pca_data[:, 0], pca_data[:, 1])
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')
plt.title('PCA of Seed Data')
plt.show()
wcss = []
for i in range(1, 11):
kmeans = KMeans(n_clusters=i, init='k-means++', max_iter=300, n_init=10, random_state=0)
kmeans.fit(pca_data)
wcss.append(kmeans.inertia_)
plt.figure(figsize=(10, 7))
plt.plot(range(1, 11), wcss)
plt.title('Elbow Method')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS')
plt.show()
kmeans = KMeans(n_clusters=3, init='k-means++', max_iter=300, n_init=10, random_state=0)
clusters = kmeans.fit_predict(pca_data)
plt.figure(figsize=(10, 7))
plt.scatter(pca_data[:, 0], pca_data[:, 1], c=clusters, cmap='viridis')
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')
plt.title('Clusters of Seed Data')
plt.show()

TODO 2
from sklearn.linear_model import Ridge, LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
data = pd.read_csv('seeds.csv')
X = data.iloc[:, :-1].values
y = data.iloc[:, -1].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
ridge_reg = Ridge(alpha=1.0)
ridge_reg.fit(X_train, y_train)
y_pred_ridge = ridge_reg.predict(X_test)
lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)
y_pred_lin = lin_reg.predict(X_test)
mse_ridge = mean_squared_error(y_test, y_pred_ridge)
mse_lin = mean_squared_error(y_test, y_pred_lin)
print(f'Ridge Regression MSE: {mse_ridge}')
print(f'Linear Regression MSE: {mse_lin}')
from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=1.0)
lasso_reg.fit(X_train, y_train)
y_pred_lasso = lasso_reg.predict(X_test)
mse_lasso = mean_squared_error(y_test, y_pred_lasso)
print(f'Lasso Regression MSE: {mse_lasso}')
from sklearn.linear_model import Ridge, LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import pandas as pd
# 데이터 로드 및 전처리
data = pd.read_csv('seeds.csv')
X = data.iloc[:, :-1].values
y = data.iloc[:, -1].values
# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# Ridge Regression 모델 학습 함수: alpha 값을 인자로 받음
def train_ridge_regression(alpha_value):
ridge_reg = Ridge(alpha=alpha_value)
ridge_reg.fit(X_train, y_train)
y_pred_ridge = ridge_reg.predict(X_test)
mse_ridge = mean_squared_error(y_test, y_pred_ridge)
return mse_ridge
# Linear Regression 모델 학습 및 성능 평가
lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)
y_pred_lin = lin_reg.predict(X_test)
mse_lin = mean_squared_error(y_test, y_pred_lin)
# Ridge Regression의 성능 평가: 여러 alpha 값에 대해 MSE 계산
alpha_values = [0.01, 0.1, 1.0, 10.0, 100.0]
for alpha_value in alpha_values:
mse_ridge = train_ridge_regression(alpha_value)
print(f'Ridge Regression MSE with alpha={alpha_value}: {mse_ridge}')
print(f'Linear Regression MSE: {mse_lin}')
TODO 1
K-means 클러스터링을 사용하여 데이터를 클러스터링합니다.
적절한 클러스터 수를 선택하기 위해 엘보우 방법(Elbow method)을 사용합니다.
PCA를 통한 차원 축소
scikit-learn의 PCA를 사용하여 데이터의 차원을 2차원으로 축소했습니다. 이를 통해 데이터를 시각화하고 분석하기 용이하게 만들었습니다. PCA 결과, 주요 두 성분이 데이터 분산의 상당 부분을 설명하는 것으로 나타났습니다.
TODO 2
Ridge Regression은 선형 회귀에 L2 규제를 추가한 모델입니다. 규제 강도는 alpha 매개변수로 조절할 수 있습니다.
Ridge Regression 모델의 MSE는 Linear Regression 모델의 MSE보다 낮게 나타났습니다. 이는 Ridge Regression이 데이터의 복잡성을 더 잘 처리하고, 과적합을 방지하는 데 효과적임을 시사합니다.
추가로 ridge를 사용하는 방법도 있지만 lasso 방법을 사용해볼 수 있습니다
사용법이 간단하여 시도해보겠습니다
0.01일 때 가장 mse가 낮으므로 성능이 제일 좋았고 신기하게 선형회귀일 때 mse가 가장 낮게 나왔습니다.
결론
밀 씨앗 데이터셋을 활용하여 클러스터링 및 차원 축소, 그리고 Regularization을 사용한 회귀 분석을 수행했습니다. PCA와 K-means 클러스터링을 통해 데이터의 구조를 이해할 수 있었습니다. 또한, Ridge Regression을 통해 데이터의 복잡성을 효과적으로 처리하고, 모델의 성능을 향상시킬 수 있었습니다. 추가로 lasso보다는 ridge의 mse 성능평가의 결과가 더 좋았습니다. 알파값의 조정에서는 낮을 값이 좀 더 좋은 성능을 나타내기도 하였습니다.
'프로젝트 > 머신러닝 과제' 카테고리의 다른 글
| [ML Project] EDA 데이터 분석 with SVM, PM, Decision Tree (2) | 2024.04.25 |
|---|---|
| [ML Project] Linear Regression을 활용한 주가 예측 모델 (0) | 2024.04.11 |